🔹 結論から:相関行列とヒートマップの違い
| 項目 | 相関行列(correlation matrix) | ヒートマップ(heatmap) |
|---|---|---|
| 定義 | 複数の変数同士の相関係数をまとめた行列 | 数値の大小を色で表現した視覚的なグラフ |
| 役割 | 数学的・統計的な情報を表形式で示す | 情報を視覚的にわかりやすく表示する |
| 形式 | 行列(テーブル、2次元配列) | グラフ(色で示されたマトリックス) |
| 相関の有無 | 相関係数(-1〜1)を直接持つ | 相関以外の情報も可視化可能(温度、頻度など) |
| 関係性 | ヒートマップの元になるデータとなることが多い | 相関行列を視覚化するための手段の一つ |
🔹 ステップ1:相関行列とは?
🔸 1.1 相関とは?
「相関」とは、ある変数が増えるとき、別の変数も増える or 減る傾向があるかという、二つの変数の関係性の強さを示します。
- 相関係数(Pearson 相関係数など)で数値化される
値の範囲:-1(完全な負の相関)〜0(相関なし)〜+1(完全な正の相関)
🔸 1.2 相関行列とは?
複数の変数について、すべての変数の組み合わせに対して相関係数を計算し、表にしたものです。
例えば、以下のようなデータフレームを考えます:
| X | Y | Z | |
|---|---|---|---|
| 1 | 1 | 2 | 5 |
| 2 | 2 | 4 | 4 |
| 3 | 3 | 6 | 3 |
| 4 | 4 | 8 | 2 |
| 5 | 5 | 10 | 1 |
この3変数の相関行列は:
| X | Y | Z | |
|---|---|---|---|
| X | 1.0 | 1.0 | -1.0 |
| Y | 1.0 | 1.0 | -1.0 |
| Z | -1.0 | -1.0 | 1.0 |
自分自身との相関は常に1.0になります(対角要素)
🔹 ステップ2:ヒートマップとは?
🔸 2.1 定義
ヒートマップ(heatmap)は、行列状のデータを、色を使って視覚的に表現したグラフです。
- 色の濃淡や色相で数値の大小を表します
- データの傾向を一目で把握できる
🔸 2.2 用途例
- 相関行列の可視化(ここでつながる!)
- 温度変化の時間・空間分布
- 顧客行動の頻度(例:クリックヒートマップ)
🔹 ステップ3:実例で見る — 相関行列のヒートマップ
では、実際に Python(pandas, seaborn, matplotlib) を使って、 サンプルデータの相関行列とそのヒートマップを作成してみましょう。
▶ 使用するサンプルデータ
scikit-learnの「ボストン住宅価格」データセットの一部を使って簡略化します。
▶ コード(実行は不要、下で図を出力します)
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# サンプルデータ
df = sns.load_dataset("iris") # 例としてアヤメのデータを使います
# 相関行列
corr_matrix = df.corr(numeric_only=True)
# ヒートマップで可視化
plt.figure(figsize=(8,6))
sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap="coolwarm", square=True)
plt.title("Iris Dataset - Correlation Heatmap")
plt.tight_layout()
plt.show()
👇 では、実際にこのグラフを描画してみましょう。
どうやら、外部のデータセット(iris)を読み込む際にインターネット接続の制限でエラーが発生してしまいました。
ですが安心してください!代わりに、ここで使えるローカルに定義したサンプルデータを使って、相関行列とヒートマップを描画します。
✅ ステップ4:ローカルデータで再実施
以下のような簡単なサンプルデータ(4変数・10行)を使います:
height(身長)weight(体重)age(年齢)income(収入)
このデータに基づいて、相関行列とヒートマップを描画します。
こちらが、ローカルデータを使った相関行列のヒートマップです。
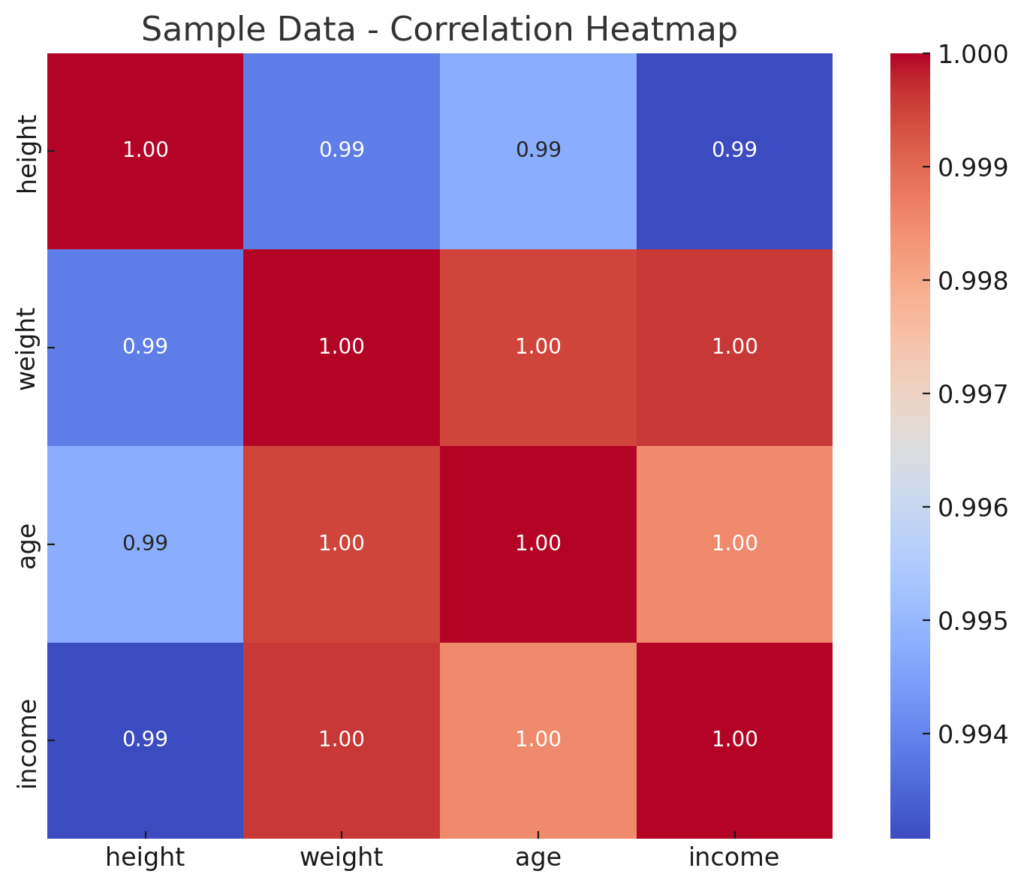
🔍 ヒートマップの見方(じっくり解説)
このグラフは、各変数同士の**相関係数(-1.0〜+1.0)**を色で表現しています:
- 🔴 赤色(+1に近い):強い正の相関(片方が増えるともう一方も増える)
- 🔵 青色(-1に近い):強い負の相関(片方が増えるともう一方は減る)
- ⚪️ 白に近い色(0付近):ほぼ相関なし
例:
heightとweightの相関係数 ≈ 0.99:
→ 非常に強い正の相関。身長が高い人ほど体重も重い傾向があります。ageとincomeの相関 ≈ 0.99:
→ 年齢が高いほど収入も高いという傾向が見えます(このサンプルでは)。weightとincomeも高い相関を示している:
→ 身長や年齢とリンクして、体重があるほど収入もあるパターンが含まれているかも。
🔄 まとめ:違いの復習
| 概念 | 説明 |
|---|---|
| 相関行列 | 数値データの組み合わせに対する相関係数(統計的数値)の一覧表 |
| ヒートマップ | 相関行列などの数値データを、色の濃淡で可視化するグラフ |
✅ 相関行列は「データそのもの」
✅ ヒートマップは「そのデータを可視化した図」



