1. クロス集計の基本概念
1.1 定義
クロス集計(英: Cross Tabulation、略してクロス表、分割表、コンティンジェンシーテーブルとも呼ばれる)とは、2つ以上のカテゴリカル変数(質的変数)間の関係を分析するための統計的手法です。具体的には、2つの変数のカテゴリ(属性)の組み合わせごとに、該当するデータがどれくらいの頻度で出現するかを表形式で表したものです。
最も基本的なクロス集計表は2次元の表で、行に一方の変数のカテゴリ、列にもう一方の変数のカテゴリを配置し、各セルにはその組み合わせに該当するケース(観測値)の数や割合が示されます。
例えば、「性別」と「購入商品カテゴリ」という2つの変数のクロス集計を行うと、男性が購入した商品カテゴリの分布と女性が購入した商品カテゴリの分布を比較することができます。
1.2 歴史的背景
クロス集計の歴史は統計学の発展と密接に関連しています。19世紀初頭、ベルギーの数学者アドルフ・ケトレーが社会現象を量的に分析するための方法として、カテゴリカルデータの集計表を用いた分析を始めたことが起源とされています。
20世紀に入ると、カール・ピアソンによるカイ二乗検定の開発(1900年)により、クロス集計表の統計的分析の基礎が確立されました。これにより、単なる記述統計から推測統計へと発展し、変数間の関連性を統計的に検証することが可能になりました。
コンピュータの発達と統計ソフトウェアの普及により、1960年代以降、クロス集計は社会調査やマーケティングリサーチなど多くの分野で標準的な分析手法として定着しました。
1.3 統計学における位置づけ
統計学の体系の中で、クロス集計は主にカテゴリカルデータ分析の基礎的手法として位置づけられています。具体的には:
- 記述統計と推測統計の橋渡し: 単純な頻度の集計(記述統計)から始まり、カイ二乗検定などの統計的検定(推測統計)へと発展させることができます。
- 探索的データ分析のツール: データの全体像を把握し、変数間の関係性を視覚的に探索するための重要な手段です。
- 多変量解析の前段階: より複雑な多変量解析(ロジスティック回帰分析、対応分析など)の前に、変数間の基本的な関係を把握するために用いられます。
- 非パラメトリック統計の一環: データの分布に関する特定の仮定を必要としない非パラメトリック手法として、幅広いデータに適用可能です。
クロス集計は、その単純さと直観的な解釈のしやすさから、統計学の専門家だけでなく、ビジネスアナリスト、医学研究者、社会科学者など様々な分野の実務家にも広く用いられています。
2. クロス集計の目的と用途
2.1 データ探索
クロス集計の第一の目的は、複数の変数間の関係性を探索的に把握することです。データ探索における具体的な用途には以下のようなものがあります:
- パターンの発見: データセット内の傾向やパターンを視覚的に発見するための手段として活用できます。例えば、特定の年齢層に特定の商品の購入傾向が強いといったパターンを見つけることができます。
- 異常値・特異値の検出: 予想外に高い(または低い)頻度を示すセルは、特別な注目や追加分析が必要な領域を示唆します。
- データの品質チェック: クロス集計によって論理的に矛盾する組み合わせ(例:「10歳未満」かつ「既婚」)などのデータエラーを発見することもできます。
- 変数間の関連性の強さの初期評価: どの変数同士が強く関連しているかを視覚的に判断し、より詳細な分析の方向性を決める手がかりとなります。
2.2 仮説検証
既存の理論や仮説を検証するためのツールとしても、クロス集計は強力です:
- 理論的予測の確認: 「若年層はオンラインショッピングを好む」といった理論的予測が実際のデータで支持されるかを検証できます。
- 統計的有意性の評価: カイ二乗検定などを用いて、観察された関連性が偶然では説明できないほど強いものかを統計的に評価します。
- 予想外の関係の検証: データ探索段階で発見された予想外のパターンについて、統計的検定を用いてその信頼性を評価します。
- 代替仮説の比較: 複数の競合する仮説がある場合、どの仮説がデータをよりよく説明するかを比較検討する基盤を提供します。
2.3 セグメント分析
市場セグメンテーションやターゲティングのための強力なツールとして利用されます:
- 顧客プロファイリング: 年齢、性別、居住地などの人口統計学的変数と購買行動の関係を分析し、顧客セグメントの特徴を把握します。
- セグメント間の比較: 異なる顧客セグメント間での行動や態度の違いを明確にし、各セグメントに適したマーケティング戦略を立案するための情報を提供します。
- ニッチ市場の特定: 全体としては小さいが、特定の条件下では重要な意味を持つ市場セグメントを特定するのに役立ちます。
- 製品開発の方向性決定: 特定の属性を持つユーザーが特に重視する機能や特徴を明らかにし、製品開発の優先順位づけに役立てます。
2.4 トレンド分析
時系列データとクロス集計を組み合わせることで、時間的変化の分析も可能になります:
- 経時的変化の把握: 同じクロス集計表を異なる時点で作成し比較することで、関係性の経時的変化を分析できます。
- 季節変動の分析: 「季節」×「購買行動」のクロス集計により、季節ごとの消費パターンの違いを明らかにできます。
- コホート分析: 特定の時期に同じ経験をした集団(コホート)ごとの行動パターンの違いを分析することができます。
- 予測モデルの基礎: 過去のトレンドに基づいて将来の傾向を予測するための基礎情報を提供します。
クロス集計は単純でありながら、これらの多様な目的に対応できる柔軟な分析ツールであり、データ分析の初期段階から高度な意思決定支援まで幅広く活用されています。
3. クロス集計表の構造と作成方法
3.1 基本構造
クロス集計表の基本構造は、以下の要素から成り立っています:
- 行変数と列変数: クロス集計表は、行方向に一つの変数(行変数)、列方向にもう一つの変数(列変数)を配置します。これらの変数はカテゴリカル(質的)変数が基本ですが、連続変数を適切に区分化(ビン化)することでも利用可能です。
- セル: 行と列の交差部分をセルと呼び、そのセルには該当する組み合わせのケース数(度数)が表示されます。
- 行合計と列合計: 表の右端と下端には、それぞれの行や列の合計値が表示されます。これらの周辺度数(マージナル)は、それぞれの変数の単純集計結果を表します。
- 総計: 表の右下隅には全ケースの合計数が表示され、データセット全体のサイズを示します。
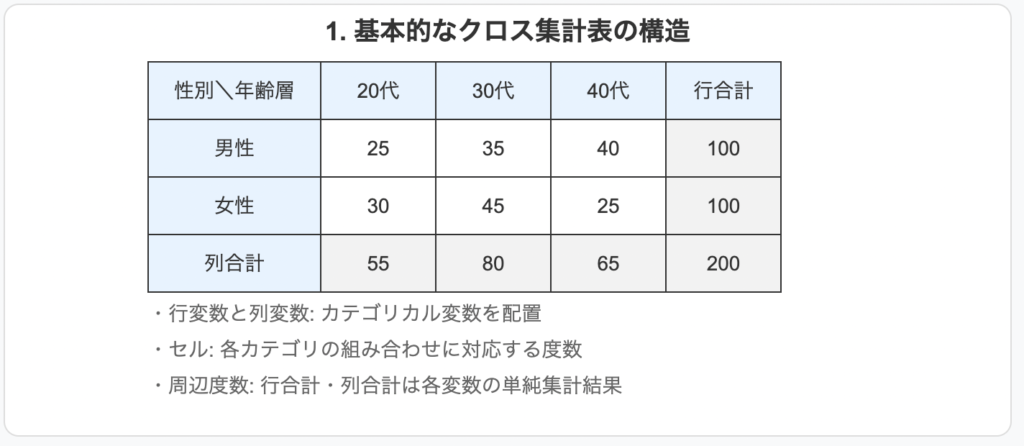
基本的なクロス集計表の構造例:
| 性別\年齢 | 20代以下 | 30代 | 40代 | 50代以上 | 行合計 |
|---|---|---|---|---|---|
| 男性 | 25 | 35 | 40 | 30 | 130 |
| 女性 | 30 | 45 | 35 | 25 | 135 |
| 列合計 | 55 | 80 | 75 | 55 | 265 |
3.2 変数の選択
クロス集計で分析する変数の選択は、分析の目的と変数の特性に基づいて行います:
- 目的との関連性: 分析目的に直接関連する変数を選択することが重要です。例えば、マーケティング施策の効果を分析する場合は、「施策の認知有無」と「購買行動」などの変数が適切です。
- 変数のタイプ:
- 名義尺度変数(性別、職業、居住地域など): 最もクロス集計に適しています。
- 順序尺度変数(満足度、学歴など): カテゴリ間に順序があるため、解釈に順序性を考慮できます。
- 間隔・比率尺度変数(年齢、所得など): 適切なカテゴリに区分化して使用します。
- カテゴリ数: 各変数のカテゴリ数はあまり多くないほうが望ましいです(一般に5~7カテゴリ程度)。カテゴリが多すぎると表が大きくなりすぎて解釈が困難になります。
- 独立変数と従属変数の区別: 因果関係を想定する場合は、独立変数(説明変数)を行または列に、従属変数(目的変数)をもう一方に配置するのが一般的です。
3.3 集計方法
クロス集計表のセルに表示する値には、以下のような選択肢があります:
- 度数(絶対数): 各セルに該当するケースの実数を表示します。最も基本的な集計方法です。
- 行パーセント: 行合計を100%として、各セルの値が行内でどのような割合を占めるかを示します。行変数のカテゴリごとに、列変数の分布を比較したい場合に有用です。
- 列パーセント: 列合計を100%として、各セルの値が列内でどのような割合を占めるかを示します。列変数のカテゴリごとに、行変数の分布を比較したい場合に有用です。
- 総パーセント: 総計を100%として、各セルの値が全体に占める割合を示します。データ全体における各組み合わせの相対的重要性を把握するのに役立ちます。
- 期待値: 独立性を仮定した場合に期待される理論上の度数です。観測値と期待値の差は関連性の強さを示す指標となります。
3.4 データ前処理
質の高いクロス集計分析のためには、適切なデータ前処理が不可欠です:
- 欠損値の処理: 欠損値を含むケースを除外するか、適切な方法で補完するかを決定します。「無回答」「該当なし」などを独立したカテゴリとして扱うこともあります。
- 外れ値の検討: 極端な値が集計結果に大きな影響を与える可能性があるため、必要に応じて対処します。
- 変数の再カテゴリ化:
- カテゴリの統合: 度数の少ないカテゴリを統合して、より意味のある分析単位を作成します。
- 連続変数の区分化: 年齢や所得などの連続変数を適切な区間に分割します。
- ウェイト付け: サンプルが母集団を正確に代表していない場合、適切なウェイト付けを行って補正することがあります。
- 派生変数の作成: 元のデータから新たな変数を作成することで、より洞察力のある分析が可能になることがあります(例:「年齢」と「性別」から「ライフステージ」変数を作成するなど)。
適切な前処理を行うことで、クロス集計の結果の信頼性と解釈可能性が大きく向上します。特に大規模なデータセットや複雑な調査データの場合、この前処理段階が分析の成否を左右する重要な要素となります。
4. クロス集計の種類
4.1 単純クロス集計
単純クロス集計は最も基本的な形式で、2つの変数間の関係を分析します:
- 特徴:
- 1つの行変数と1つの列変数のみを使用
- 二次元の表形式で表現
- 最も一般的に使用されるクロス集計の形式
- 適用例:
- 「性別」×「商品購入有無」
- 「年齢層」×「サービス満足度」
- 「居住地域」×「政党支持」
- 利点:
- 理解しやすく解釈が直感的
- 作成が容易
- 視覚的に関係性を把握しやすい
- 限界:
- 第三の変数の影響(交絡因子)を考慮できない
- 複雑な関係性を捉えられない場合がある
4.2 多重クロス集計
多重クロス集計は、3つ以上の変数間の関係を分析するために使用されます:
- 特徴:
- 3つ以上の変数を同時に分析
- 三次元以上の表として概念化されるが、実際には層別化された二次元表として表現されることが多い
- 表現方法:
- 層別法: 第三の変数(層変数)のカテゴリごとに別々の二次元クロス表を作成
- 入れ子構造: 行または列の中に別の変数のカテゴリを入れ子にする
- パネル表示: 複数の二次元表をパネルとして配置
- 適用例:
- 「性別」×「年齢層」×「商品購入有無」
- 「教育水準」×「職業」×「収入レベル」×「政治的立場」
- 利点:
- 交絡因子の影響を制御できる
- より複雑な関係性やパターンを発見できる
- シンプソンのパラドックスを検出できる
- 限界:
- 解釈が複雑になる
- カテゴリ数が増えるとセルの度数が少なくなり、統計的信頼性が低下する
- 表現が煩雑になりやすい
4.3 条件付きクロス集計
条件付きクロス集計は、特定の条件を満たすケースのみを対象として分析を行います:
- 特徴:
- データセットの一部(サブセット)のみを対象とする
- フィルタリング条件を適用してから集計を行う
- 条件の例:
- 「購入経験あり」の回答者のみを対象
- 「30歳以上」の回答者のみを対象
- 「特定地域の居住者」のみを対象
- 適用例:
- 「サービス利用者のみ」を対象とした「利用頻度」×「満足度」の分析
- 「高所得層のみ」を対象とした「年齢」×「投資行動」の分析
- 利点:
- 特定のセグメントに焦点を当てた詳細分析が可能
- 全体では見えにくいパターンを発見できる
- 条件による差異を明確にできる
- 注意点:
- サンプルサイズが減少するため統計的検出力が低下する
- 選択バイアスの可能性がある
- 条件設定の妥当性が結果の信頼性に直結する
4.4 時系列クロス集計
時系列クロス集計は、時間的変化を分析するためのクロス集計の応用形式です:
- 特徴:
- 時間的要素(年、四半期、月など)を変数の一つとして含む
- 経時的な変化やトレンドを把握するために用いられる
- 表現方法:
- 時間を列変数として: 各時点をカラムとして配置し、行変数の分布の時間的変化を分析
- 時間を層変数として: 各時点ごとに別々のクロス表を作成して比較
- 適用例:
- 「四半期」×「商品カテゴリ」×「売上高」
- 「年度」×「顧客セグメント」×「顧客満足度」
- 「選挙年」×「年齢層」×「投票行動」
- 利点:
- 経時的変化を視覚的に把握できる
- 季節性や周期性を検出できる
- トレンドの転換点を特定できる
- 分析手法:
- トレンド分析: 長期的な上昇・下降傾向の把握
- 季節変動分析: 周期的なパターンの検出
- イベント影響分析: 特定イベント前後の変化の測定
時系列クロス集計は、特にマーケティング、経済分析、社会変動研究などで重要な役割を果たし、単なる静的な関係性の把握を超えて、動的な変化のパターンを明らかにすることができます。
5. クロス集計表の読み方と分析技法
5.1 基本的な読み方
クロス集計表から情報を効果的に読み取るための基本的なアプローチには以下があります:
- 全体像の把握:
- まず表全体を概観し、総計やサンプルサイズを確認する
- データの分布の偏りや特徴を大まかに把握する
- 行変数と列変数の分布:
- 行合計と列合計(周辺分布)を見て、各変数の単純分布を確認する
- 不均衡な分布がある場合、解釈に注意する
- 特定のセルに注目:
- 特に高い値や低い値を示すセルを特定する
- 予想と一致しない「意外な」セルに注目する
- 対角線と非対角線のパターン:
- 対称的なクロス表では、対角線に沿ったパターンが特定の関係を示すことがある
- 非対角線上の値が高い場合、逆相関の可能性を示唆する
- 読み取りの方向性:
- 行パーセントを使用する場合は行方向に読む(各行内での分布を比較)
- 列パーセントを使用する場合は列方向に読む(各列内での分布を比較)
5.2 比率の分析
比率(パーセンテージ)を用いた分析は、クロス集計表の解釈を容易にします:
- 行パーセント分析:
- 計算方法: (セルの度数 ÷ 行合計) × 100
- 用途: 行変数の各カテゴリにおける列変数の分布を比較
- 例: 各年齢層ごとの商品購入率の比較
- 列パーセント分析:
- 計算方法: (セルの度数 ÷ 列合計) × 100
- 用途: 列変数の各カテゴリにおける行変数の分布を比較
- 例: 各商品カテゴリの購入者における性別構成比の比較
- 総パーセント分析:
- 計算方法: (セルの度数 ÷ 総計) × 100
- 用途: 全体におけるセルの相対的重要性の評価
- 例: 全回答者における「30代男性」の割合
- 適切な比率の選択:
- 因果関係の想定方向に基づいて選択(独立変数のカテゴリ間で従属変数の分布を比較)
- 比較したい対象に応じて選択(グループ間比較なら行/列パーセント、全体での位置づけなら総パーセント)
5.3 インデックス分析
インデックス(指数)分析は、観測値と期待値の比較により関連性の強さを測定します:
- インデックスの計算:
- 基本式: (実際の度数 ÷ 期待度数) × 100
- 期待度数 = (行合計 × 列合計) ÷ 総計
- インデックス値の解釈:
- 100 = 期待通りの関連性(独立性仮説と一致)
- 100超 = 正の関連性(期待よりも強い関係)
- 100未満 = 負の関連性(期待よりも弱い関係)
- インデックスの視覚化:
- ヒートマップや色分けされたクロス表での表現
- グラデーションカラーによる強度の表現
- 適用例:
- マーケティングにおける親和性分析
- メディア接触と購買行動の関連性分析
- 地域×疾病発生率の偏差分析
5.4 期待値との比較
期待値との比較は、変数間の独立性からの逸脱を評価する方法です:
- 期待値の計算:
- 期待度数 = (行合計 × 列合計) ÷ 総計
- 独立性を仮定した場合に理論的に期待される値
- 残差の分析:
- 単純残差 = 観測度数 – 期待度数
- 標準化残差 = 単純残差 ÷ √期待度数
- 調整済み標準化残差 = 単純残差 ÷ √(期待度数 × (1-行比率) × (1-列比率))
- 残差の解釈:
- 正の残差 = 期待よりも多い(正の関連)
- 負の残差 = 期待よりも少ない(負の関連)
- 絶対値が大きいほど関連が強い
- 統計的有意性:
- 調整済み標準化残差の絶対値が1.96以上で5%水準で有意
- 調整済み標準化残差の絶対値が2.58以上で1%水準で有意
- 残差分析の視覚化:
- 残差に基づいたセルの色分け
- 気泡の大きさで残差の大きさを表現するバブルプロット
これらの分析技法を組み合わせることで、クロス集計表から単なる数値の羅列以上の洞察を得ることができます。特に、比率分析とインデックス分析を併用することで、データの構造をより多角的に理解することが可能になります。
6. 統計的検定とクロス集計
6.1 カイ二乗検定
カイ二乗検定は、クロス集計表における変数間の独立性を検証するための最も基本的な統計的検定です:
- 基本概念:
- 帰無仮説: 二つの変数間に関連性がない(独立している)
- 対立仮説: 二つの変数間に関連性がある(独立でない)
- 検定統計量の計算:
- χ² = Σ[(O – E)² / E]
- O: 観測度数(実際のセル値)
- E: 期待度数(独立性を仮定した場合の理論値)
- 自由度:
- df = (行カテゴリ数 – 1) × (列カテゴリ数 – 1)
- 検定統計量の分布を決定する重要なパラメータ
- p値の解釈:
- p < 0.05: 有意水準5%で帰無仮説を棄却(関連性あり)
- p < 0.01: 有意水準1%で帰無仮説を棄却(強い関連性あり)
- p ≥ 0.05: 帰無仮説を棄却できない(関連性を証明できない)
- 前提条件と制約:
- 全てのセルの期待度数が5以上であることが望ましい
- 期待度数が5未満のセルが全体の20%を超える場合、検定結果の信頼性が低下
- サンプルサイズが十分に大きいこと(通常30以上)
6.2 フィッシャーの正確確率検定
フィッシャーの正確確率検定は、特に小サンプルの2×2クロス表に適した検定方法です:
- 適用条件:
- サンプルサイズが小さい場合
- 期待度数が5未満のセルが多い場合
- 特に2×2の分割表での分析に適している
- 検定の原理:
- 周辺度数を固定した条件付き確率の計算
- 超幾何分布に基づく正確な確率計算
- 計算方法:
- 2×2表における確率: p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
- a,b,c,d: 各セルの度数、n: 総数
- 観測された表と同じかそれより極端な表の確率の合計
- 両側検定と片側検定:
- 両側検定: 関連性の有無を検証
- 片側検定: 特定の方向の関連性を検証
- 拡張版:
- Freeman-Halton拡張: 2×3や3×3などより大きな表にも適用可能
6.3 残差分析
残差分析は、クロス集計表の個々のセルにおける関連性を詳細に検討する方法です:
- 標準化残差:
- 計算式: (観測度数 – 期待度数) / √期待度数
- 解釈: 標準正規分布に近似的に従う統計量
- 調整済み標準化残差:
- 計算式: (観測度数 – 期待度数) / √[期待度数 × (1 – 行比率) × (1 – 列比率)]
- 特徴: 周辺分布の影響を調整した、より正確な指標
- 有意水準の判断:
- |z| > 1.96: 5%水準で有意
- |z| > 2.58: 1%水準で有意
- |z| > 3.29: 0.1%水準で有意
- 多重比較問題:
- 多数のセルを同時に検定する場合の偽陽性リスク
- Bonferroni補正などによる調整の必要性
- 視覚化:
- ヒートマップによる残差の視覚化
- 色の濃さで関連の強さを表現
6.4 クラメールのV係数
クラメールのV係数は、クロス集計表における関連性の強さを測定する効果量指標です:
- 計算式:
- V = √(χ² / [n × min(r-1, c-1)])
- n: 総サンプル数
- r: 行数、c: 列数
- 値の範囲と解釈:
- 0 ≤ V ≤ 1
- 0: 関連性なし
- 1: 完全な関連性
- 一般的な目安:
- 0.1未満: 無視できる関連性
- 0.1-0.3: 弱い関連性
- 0.3-0.5: 中程度の関連性
- 0.5以上: 強い関連性
- 特徴:
- サンプルサイズの影響を受けにくい
- 異なるサイズのクロス表間で比較可能
- 非対称的な表でも適用可能
- その他の関連指標:
- ファイ係数: 2×2表の場合のみ適用
- 分割係数: カテゴリカル変数間の関連性を測定する別の指標
- コンティンジェンシー係数: 標準化されていないため解釈に注意が必要
これらの統計的検定と効果量指標を適切に組み合わせることで、クロス集計分析の信頼性と解釈の深さを大幅に向上させることができます。特に、単に関連性の有無を検定するだけでなく、その関連性の強さや個々のセルレベルでの特異性を評価することが、高品質なクロス集計分析には不可欠です。
7. クロス集計の視覚化
7.1 ヒートマップ
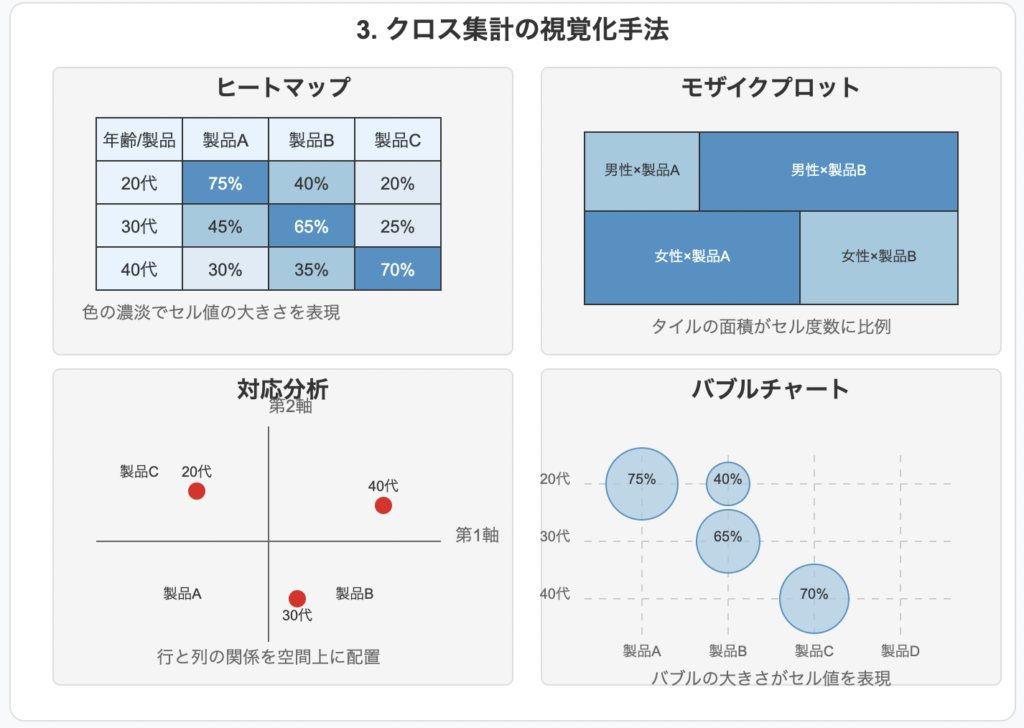
ヒートマップは、クロス集計表のセル値を色の濃淡で表現する視覚化手法です:
- 基本原理:
- 数値の大小を色の濃淡やグラデーションで表現
- 高い値=濃い色、低い値=薄い色という対応関係
- 適用可能なデータ:
- 度数(絶対数)
- パーセンテージ
- 標準化残差
- インデックス値
- 色選択のポイント:
- 単調増加データ: 単色グラデーション(例: 白→青)
- 正負両方のデータ: 二色グラデーション(例: 青→白→赤)
- カラーユニバーサルデザインへの配慮
- 利点:
- パターンの視覚的把握が容易
- 大規模な表でも全体像を掴みやすい
- 異常値や特徴的なセグメントの発見が容易
- 実装ツール:
- Excel条件付き書式
- R(heatmap関数)
- Python(seaborn.heatmap)
- Tableau、Power BIなどのBI
7.2 モザイクプロット
モザイクプロットは、セルの面積でデータの比率を表現する高度な視覚化手法です:
- 基本原理:
- 各セルの面積がそのセルの度数に比例
- 行変数・列変数の周辺分布も同時に表現可能
- 構成要素:
- タイルの大きさ: セルの相対的頻度
- タイルの色: 標準化残差などの指標(オプション)
- 区分線: 変数のカテゴリ境界
- 解釈のポイント:
- 大きなタイル: 頻度の高い組み合わせ
- 色付きタイル: 期待値との乖離が大きいセル
- 整列したタイル: 独立性を示唆
- 利点:
- 度数と残差を同時に表現できる
- 周辺分布の偏りを視覚的に認識できる
- 3つ以上の変数も表現可能
- 実装ツール:
- R(vcd::mosaic)
- Python(statsmodels.graphics.mosaicplot)
- JMP(モザイクプロット機能)
7.3 バブルチャート
バブルチャートは、クロス集計表の各セルを散布図上の円として表現する手法です:
- 基本構造:
- X軸: 列変数のカテゴリ
- Y軸: 行変数のカテゴリ
- バブルの大きさ: セルの度数や割合
- バブルの色: 別の指標(オプション)
- バリエーション:
- シンプルバブルチャート: 大きさのみでデータを表現
- カラーバブルチャート: 色でインデックスや残差を表現
- 多変量バブルチャート: 第3、第4の変数を色や形で表現
- 利点:
- 直感的で理解しやすい
- 大きさの違いがパターンを明確に示す
- カスタマイズの自由度が高い
- 注意点:
- バブルサイズの調整が重要(小さすぎず大きすぎず)
- 0値や欠損値の表示方法の検討
- 軸の順序が解釈に影響する
- 実装ツール:
- Excel(散布図のバブルサイズ調整)
- Tableau(バブルチャート機能)
- R(ggplot2::geom_point with size)
- Python(matplotlib or plotly)
7.4 対応分析
対応分析は、クロス集計表の行と列のカテゴリ間の関係を二次元空間上に視覚化する多変量解析手法です:
- 基本原理:
- 行カテゴリと列カテゴリを同一の空間上に配置
- 距離が近いほど関連性が強い
- 原点からの距離が遠いほど特徴的(平均的プロファイルから乖離)
- 技術的基盤:
- 特異値分解(SVD)に基づく次元削減手法
- カイ二乗距離を用いた距離測定
- 解釈のポイント:
- 近接するカテゴリ同士: 強い関連性
- 原点付近のカテゴリ: 平均的なプロファイル
- 軸の解釈: 主要な変動要因を表す
- 寄与率: 各軸がどれだけ情報を保持しているか
- 適用例:
- 市場セグメンテーション分析
- ブランドポジショニング
- テキストマイニング(単語と文書の関係)
- 発展形:
- 多重対応分析: 3つ以上の変数に対応
- 正準対応分析: 環境要因との関連分析に適用
- 実装ツール:
- R(ca, FactoMineR)
- Python(prince, sklearn.decomposition)
- SPSS(ANACOR)
- SAS(PROC CORRESP)
これらの視覚化技法は単独でも有効ですが、分析の目的や対象とするデータの特性に応じて複数の手法を組み合わせることで、より豊かな洞察を得ることができます。特に、基本的なヒートマップから始めて、より高度なモザイクプロットや対応分析へと段階的に分析を深めていくアプローチが効果的です。
8. クロス集計における注意点と落とし穴
8.1 サンプルサイズの問題
クロス集計分析では、サンプルサイズが結果の信頼性に大きく影響します:
- 少数セルの問題:
- セル内のケース数が少ない場合(一般に5未満)、統計的検定の信頼性が低下
- 解決策:
- カテゴリの統合による表の縮小
- フィッシャーの正確確率検定の使用
- サンプルサイズの増加
- 希薄データマトリックス:
- 多くのセルに0や極めて小さい値が含まれる場合
- 特に多カテゴリ変数や多変量クロス集計で発生
- 解決策:
- 次元削減(主成分分析、対応分析など)
- 階層的クラスタリングによるカテゴリ統合
- サンプルサイズと統計的有意性:
- 大規模サンプルでは統計的に有意でも実質的意義が小さい場合がある
- 小規模サンプルでは実質的に重要な関係も有意にならない場合がある
- 対策:
- 効果量(クラメールのV係数など)の併用
- 実質的意義と統計的有意性の両面からの評価
- 信頼区間の検討:
- セルのパーセンテージに対する信頼区間の計算
- 特に比較的小さいサンプルでの解釈には信頼区間を考慮
8.2 因果関係と相関関係の混同
クロス集計表から観察される関連性を因果関係と誤解釈するリスクがあります:
- 相関≠因果の原則:
- クロス集計で観察される関連性は、変数間の相関関係を示すのみ
- 因果関係の特定には、さらなる条件(時間的先行性、代替説明の排除など)が必要
- 共変量(交絡因子)の問題:
- 第三の変数が両方の変数に影響し、見かけ上の関連を生じさせる可能性
- 対策:
- 層別解析(第三変数でデータを層別してクロス集計)
- 多変量解析(ロジスティック回帰など)との併用
- DAG(Directed Acyclic Graph)による因果モデルの検討
- 選択バイアス:
- サンプルの選択方法が結果に影響する可能性
- 例: 特定の属性を持つ人が調査に参加しやすい場合
- 対策:
- ランダムサンプリングの徹底
- ウェイト調整
- 非回答バイアスの分析
- 反事実的思考の必要性:
- 「もし原因が存在しなかったら、結果はどうなっていたか」という視点
- クロス集計だけでは反事実的シナリオの評価は困難
8.3 シンプソンのパラドックス
シンプソンのパラドックスは、全体のデータで見られる関係性が、データを層別すると逆転する現象です:
- パラドックスの本質:
- 集約データに基づく分析と層別データに基づく分析で、結論が相反する
- 第三の変数(層別変数)との関連が強い場合に発生しやすい
- 古典的事例:
- バークレイ大学の大学院入学選考
- 男女別の手術成功率の比較
- 喫煙と病気の関係の年齢調整
- 検出方法:
- 可能な限り多くの関連変数で層別分析を実施
- 全体の関連と層別後の関連を常に比較
- 理論的に重要な第三変数の事前特定
- 対策:
- 多変量クロス集計による層別分析
- グラフィカルモデル(DAG)による変数間関係の可視化
- 潜在クラス分析などの高度な統計モデルの活用
8.4 多重比較問題
多くのセルを同時に検定する場合、偶然による偽陽性のリスクが高まります:
- 問題の本質:
- 多数の統計的検定を同時に行うと、偶然に有意な結果が出る確率が増加
- 例: 5%有意水準で20の検定を行うと、偶然に少なくとも1つが有意になる確率は約64%
- 影響:
- 大きなクロス表での残差分析
- 多変量クロス集計での複数の関連性検定
- 探索的分析での多数の組み合わせ検討
- 調整方法:
- Bonferroni補正: p値にテスト数を乗じる(最も保守的)
- Holm法: より検出力の高い段階的補正
- False Discovery Rate(FDR)制御: 偽発見率を制御する方法
- 実用的アプローチ:
- 事前仮説の明確化(探索vs確認)
- 効果量の大きさも考慮した総合判断
- 複数のデータセットやサンプルでの検証(再現性)
これらの注意点と落とし穴を理解し適切に対処することで、クロス集計分析の信頼性と妥当性を大幅に向上させることができます。特に、単純なクロス表の解釈に留まらず、交絡因子の影響やシンプソンのパラドックスの可能性を常に意識することが、誤った結論を避けるための鍵となります。
9. 高度なクロス集計技法
9.1 ログリニアモデル
ログリニアモデルは、多次元クロス集計表の解析のための強力な統計モデルです:
- 基本原理:
- セルの対数期待度数を変数の主効果と交互作用効果の線形和としてモデル化
- log(期待度数) = 全体平均効果 + 変数Aの主効果 + 変数Bの主効果 + … + 変数A×Bの交互作用 + …
- モデルの種類:
- 飽和モデル: すべての交互作用を含む
- 階層モデル: 高次の交互作用を順次除外
- 独立モデル: 交互作用を含まない
- 条件付き独立モデル: 特定の交互作用のみを含む
- モデル選択:
- 尤度比統計量を用いたモデル比較
- AIC、BICなどの情報量規準
- ステップワイズ法による最適モデル探索
- 利点:
- 複雑な多次元表を統一的に分析可能
- 交互作用を定量的に評価可能
- 条件付き独立性の検討に有用
- 適用例:
- 複数の社会経済変数間の複雑な関連性分析
- マルチチャネルマーケティングの効果分析
- 医学研究での多因子リスク評価
9.2 対応分析の応用
対応分析の高度な応用形態は、複雑なカテゴリカルデータの構造を解明するのに役立ちます:
- 多重対応分析(MCA):
- 3つ以上のカテゴリカル変数の関係を同時に分析
- 調査データの質問項目間の関係性の視覚化に最適
- ディスジョイント・テーブル(各ケースが各変数で1つのカテゴリに所属)に適用
- 非対称対応分析:
- 行と列が非対称的な関係にある場合(例:従属・独立関係)
- 消費者と商品、患者と症状など非対称な関係の分析に適用
- 条件付き確率に基づく距離測定
- 正準対応分析(CCA):
- 2つのカテゴリカル変数群間の関係を分析
- 生態学でのサイト×種×環境要因の分析に頻用
- 変数群間の相関を最大化する軸を見つける
- 部分最小二乗回帰との組み合わせ:
- 潜在構造モデリングとの融合
- 予測モデルとしての活用
- 高次元データの削減と構造化
9.3 潜在クラス分析との組み合わせ
潜在クラス分析とクロス集計の組み合わせにより、隠れた群構造を明らかにできます:
- 潜在クラス分析の基本:
- 観測されたカテゴリカル変数の背後に潜む隠れた分類を特定
- 条件付き独立性の仮定に基づく確率モデル
- 混合分布モデルのカテゴリカルデータ版
- クロス集計との連携:
- 潜在クラスをクロス集計の層変数として利用
- 複雑なパターンを潜在クラスごとに単純化
- シンプソンのパラドックスの解消
- セグメンテーションへの応用:
- データ主導型の顧客セグメント特定
- 各セグメント内での変数関連性の分析
- 行動パターンに基づく隠れた群の発見
- 実装ツール:
- R(poLCA)
- Mplus
- Latent GOLD
9.4 機械学習との連携
機械学習技術とクロス集計を組み合わせることで、より高度な分析が可能になります:
- 決定木との連携:
- CARTやCHAIDアルゴリズムによる自動的な最適分割変数の特定
- クロス集計の変数選択やカテゴリ統合の最適化
- 木構造の各ノードでのクロス集計による詳細分析
- アソシエーション分析:
- マーケットバスケット分析の手法をクロス集計に応用
- 支持度、確信度、リフト値などの指標による関連性評価
- 予期せぬ項目間の関連性の発見
- ランダムフォレスト変数重要度:
- 多数の変数からクロス集計に含めるべき重要変数の特定
- 非線形関係や複雑な交互作用の探索
- 変数重要度に基づくクロス集計の階層化
- クラスタリングとクロス集計:
- ケースのクラスタリング結果をクロス集計の変数として利用
- 類似パターンを持つケースのグループ内での関連性分析
- k-meansやHCなどの手法との組み合わせ
- 次元削減技術との連携:
- 主成分分析や因子分析で抽出した因子を用いたクロス集計
- t-SNEやUMAPで二次元に圧縮したデータとカテゴリの関係分析
- 高次元データの構造をクロス集計で解釈
これらの高度な技法は、従来のクロス集計の限界を超えて、より複雑なデータ構造を解明し、より深い洞察を得るための強力なツールとなります。特に、大規模で複雑なデータセットの分析において、これらの手法の組み合わせは相乗効果を生み出します。
10. 業界別クロス集計の活用事例
10.1 マーケティングリサーチ
マーケティング分野では、クロス集計が消費者行動の理解と戦略立案に不可欠です:
- 顧客セグメンテーション:
- 人口統計変数×購買行動のクロス集計
- ライフスタイル特性×ブランド選好のパターン分析
- 価格感度×品質重視度による市場セグメント特定
- 製品開発支援:
- 顧客属性×製品機能重視度のクロス分析
- 不満点×顧客層の分析による改善ポイントの特定
- 競合製品利用経験×自社製品評価のギャップ分析
- コミュニケーション戦略最適化:
- メディア接触×購買意向のクロス集計
- メッセージ訴求ポイント×顧客層の反応分析
- SNS利用パターン×情報拡散行動の関連性分析
- 価格戦略策定:
- 価格感度×所得層のクロス集計
- 価格帯別購入頻度×顧客層分析
- 値引き反応性×ロイヤルティのマトリクス分析
- 実例:
- 飲料メーカーによる「年齢層×時間帯×購入場所」の多重クロス集計による販売戦略最適化
- 自動車メーカーの「ライフステージ×重視機能×予算」クロス分析によるモデル開発
- 小売業の「購買頻度×買上金額×商品カテゴリ」クロス集計によるCRM戦略策定
10.2 医学・疫学研究
医学・疫学分野では、クロス集計が疾病の要因分析や治療効果の評価に活用されています:
- リスク因子分析:
- 生活習慣要因×疾患発症率のクロス集計
- 遺伝的要因×環境要因×疾患重症度の多重クロス分析
- 年齢層×性別×疾患種類の疫学的パターン分析
- 治療効果評価:
- 治療法×治癒率のクロス集計(対照群との比較)
- 患者背景要因×治療反応性の関連分析
- 併用薬×副作用発現率のクロス表による安全性評価
- 医療サービス最適化:
- 患者属性×医療サービス利用パターンのクロス分析
- 地域×疾患×医療リソース利用のクロス集計
- 保険種別×治療コスト×治療成績の関連性評価
- 公衆衛生政策支援:
- 社会経済的要因×健康行動×健康指標のクロス分析
- 地域×予防接種率×感染症発生率の関連評価
- 健康啓発施策×健康意識×行動変容のクロス集計
- 実例:
- COVID-19パンデミック時の「年齢層×基礎疾患×重症化率」クロス分析による優先接種戦略策定
- がん研究における「生活習慣要因×遺伝的リスク×発症率」の層別クロス集計
- 精神医学研究での「治療法×患者背景×再発率」クロス集計による個別化医療の推進
10.3 社会調査
社会学や政治学の調査では、クロス集計が社会現象の理解に重要な役割を果たします:
- 世論調査分析:
- 年齢層×性別×政治的立場のクロス集計
- 教育水準×社会的課題への意識のパターン分析
- 地域×所得層×政策支持度の関連性評価
- 社会変動分析:
- 時系列×社会階層×価値観変化のクロス分析
- 世代×家族構成×ライフスタイルの変化追跡
- 出生コホート×ライフイベント経験のクロス集計
- 社会問題の構造理解:
- 社会経済的要因×差別経験のクロス集計
- 地域×教育機会×社会移動性の関連分析
- 家庭環境×教育達成×キャリア形成のパス分析
- 政策効果測定:
- 政策介入前後×対象層×効果指標のクロス集計
- 地域×政策実施強度×社会指標の改善度分析
- 受益者属性×政策評価のマトリクス分析
- 実例:
- 選挙調査における「年齢×教育×投票行動」クロス集計による有権者行動分析
- 社会資本研究での「地域×信頼度×市民参加」クロス分析
- ジェンダー研究における「職業×性別×賃金格差」の時系列クロス集計
10.4 品質管理
製造業や品質管理分野では、クロス集計が不良品の原因究明や品質改善に活用されています:
- 不良要因分析:
- 製造条件×不良タイプのクロス集計
- 原材料ロット×工程パラメータ×不良率の多重クロス分析
- 作業者×機械×不良発生パターンの関連性評価
- 品質特性の関連性分析:
- 品質特性間のクロス集計による相互関連の把握
- 工程パラメータ×品質特性のマトリクス分析
- 設計要因×性能指標のクロス集計
- 顧客クレーム分析:
- 製品カテゴリ×クレーム内容のクロス集計
- 使用環境×故障モードの関連性分析
- 製造時期×故障発生時期のクロス表分析
- 工程能力改善:
- 工程パラメータ×ばらつき指標のクロス集計
- 改善施策×不良率低減効果の前後比較
- 管理手法×品質指標のマトリクス評価
- 実例:
- 自動車製造での「部品サプライヤー×組立工程×不具合率」クロス分析
- 半導体製造における「ウェハロット×プロセス条件×歩留まり」クロス集計
- 食品製造での「原料産地×製造ライン×品質スコア」の関連性評価
これらの業界別事例は、クロス集計が単なる統計手法を超えて、実務的な問題解決や意思決定支援に不可欠なツールであることを示しています。各業界の特性に合わせたクロス集計の適用と解釈のノウハウを蓄積することで、より効果的なデータ活用が可能になります。
11. クロス集計のためのツールとソフトウェア
11.1 統計ソフトウェア
専門的な統計分析ソフトウェアは、高度なクロス集計機能を提供します:
- SPSS:
- 特徴: ユーザーフレンドリーなインターフェース、包括的なクロス集計機能
- 主な機能:
- 「クロス集計表」プロシージャで多様な統計量を計算
- 調整済み残差、カイ二乗検定、ファイ係数などの自動計算
- 多重回答セットのクロス集計
- 強み: 社会科学研究向けの充実した機能
- SAS:
- 特徴: エンタープライズレベルの堅牢な分析環境
- 主な機能:
- PROC FREQによる高度なクロス集計
- 複雑なサンプリングデザインを考慮した分析
- CMH検定など高度な統計検定の実装
- 強み: 大規模データ処理と高度な統計解析
- R:
- 特徴: オープンソース、拡張性の高さ
- 主な機能:
- base::tableやstats::xtabs関数による基本集計
- gmodels::CrossTableによる詳細な統計量表示
- vcd、caporパッケージによる視覚化と対応分析
- 強み: カスタマイズ性の高さと最新手法の実装
- Stata:
- 特徴: 計量経済学や疫学研究に強み
- 主な機能:
- tabulate, tabulateコマンドによるクロス集計
- svy接頭辞による複雑なサンプリング設計の考慮
- 高度な後処理オプション
- 強み: 疫学研究向けの機能と簡潔なシンタックス
11.2 ビジネスインテリジェンスツール
ビジネス向けのデータ分析・可視化ツールもクロス集計機能を提供しています:
- Tableau:
- 特徴: 直感的な操作性とインタラクティブな視覚化
- クロス集計機能:
- ドラッグ&ドロップでのクロス表作成
- ヒートマップやハイライトテーブルの簡単作成
- ダッシュボードへの組み込みと対話的フィルタリング
- 強み: ビジュアル分析と共有のしやすさ
- Power BI:
- 特徴: Microsoftエコシステムとの統合
- クロス集計機能:
- マトリックスビジュアルによるクロス集計
- DAX言語による高度な計算の追加
- ドリルダウン機能によるデータ探索
- 強み: コスト効率と企業データとの連携のしやすさ
- QlikView/Qlik Sense:
- 特徴: アソシエーティブデータモデル
- クロス集計機能:
- ピボットテーブルによるインタラクティブなクロス集計
- メモリ内分析による高速な集計処理
- 選択による動的なデータフィルタリング
- 強み: アドホックな分析と探索的データ分析
- Looker:
- 特徴: モデル駆動型アプローチ
- クロス集計機能:
- LookML言語によるピボットテーブル定義
- 動的なフィールド選択と集計
- 埋め込み可能なクロス集計表
- 強み: データガバナンスと一貫した定義
11.3 プログラミング言語とライブラリ
プログラミング言語とその拡張ライブラリは、柔軟なクロス集計分析を可能にします:
- Python:
- 主要ライブラリ:
- pandas:
crosstabやpivot_table関数 - statsmodels: 統計検定と残差分析
- scipy.stats: 統計的検定
- seaborn: ヒートマップなどの視覚化
- pandas:
- 強み: データサイエンスパイプラインとの統合と自動化
- 主要ライブラリ:
- JavaScript/D3.js:
- 特徴: Webベースの対話的視覚化
- 関連ライブラリ:
- crossfilter.js: 高速なクロス集計とフィルタリング
- d3.js: カスタム視覚化の作成
- dc.js: 対話的なダッシュボード
- 強み: Webアプリケーションへの組み込みやすさ
- SQL:
- 特徴: データベース内での直接集計
- 実現方法:
- PIVOT機能(SQLServer)
- CASE WHEN構文とGROUP BY
- クロス表生成用のストアドプロシージャ
- 強み: 大規模データでの高パフォーマンス
- Julia:
- 特徴: 高性能な科学技術計算
- 関連パッケージ:
- FreqTables.jl
- DataFrames.jl
- HypothesisTests.jl
- 強み: 計算集約型分析での高速性
11.4 専用クロス集計ツール
特定の業界や目的に特化したクロス集計ツールも存在します:
- 市場調査専用ツール:
- Q Research Software
- Displayr
- Qualtrics Stats iQ
- WINCROSS
- 強み: 調査データに特化した機能(ウェイト付け、多重回答処理など)
- オンライン分析処理(OLAP)ツール:
- Microsoft Analysis Services
- Oracle OLAP
- IBM Cognos TM1
- 強み: 多次元データの高速なスライス・アンド・ダイス
- テキストマイニング統合型:
- SPSS Text Analytics
- RapidMiner Text Mining Extension
- KH Coder
- 強み: テキストデータとカテゴリカルデータの統合分析
- 調査会社プラットフォーム:
- Confirmit
- Decipher
- SurveyMonkey Analyze
- 強み: 調査設計から分析までのエンドツーエンド機能
これらのツールとソフトウェアは、分析者のスキルレベル、予算、分析の複雑さ、そして組織のITインフラに応じて選択すべきです。多くの場合、基本的なクロス集計は表計算ソフト(Excel、Googleスプレッドシート)でも実施可能ですが、より高度な分析や大規模データの処理には専用ツールの利用が推奨されます。
12. 実践演習:ステップバイステップのクロス集計分析
12.1 問題設定
実践的なクロス集計分析を行うための問題設定を考えてみましょう:
- ビジネスケース:
- オンライン小売業者が、自社のECサイトの顧客購買行動を分析し、マーケティング戦略を最適化したい
- 特に、顧客の年齢層、性別、購入頻度、購入カテゴリ、客単価の関連性を理解したい
- 研究課題:
- どの顧客セグメントが最も高い客単価を示すか?
- 年齢層と性別によって購入カテゴリの好みはどう異なるか?
- 購入頻度と客単価の間にはどのような関係があるか?
- 時間帯によって購入する顧客層に違いはあるか?
- データ概要:
- サンプルサイズ: 3,000顧客
- 収集期間: 過去6ヶ月間のトランザクションデータ
- 主要変数: 年齢層、性別、購入頻度、主要購入カテゴリ、平均客単価、主な購入時間帯
12.2 データ準備
実際の分析に先立ち、データの準備と前処理を行います:
- 変数の定義と区分化:
- 年齢層: 10代、20代、30代、40代、50代、60代以上
- 購入頻度: 低頻度(3ヶ月に1回未満)、中頻度(月1~2回)、高頻度(週1回以上)
- 客単価: 低(3,000円未満)、中(3,000~10,000円)、高(10,000円超)
- 購入カテゴリ: 衣料品、家電、食品・飲料、美容・健康、書籍・メディア
- 購入時間帯: 朝(6-10時)、昼(10-14時)、午後(14-18時)、夕方(18-22時)、深夜(22-6時)
- データクリーニング:
- 欠損値の処理: 重要変数に欠損のあるケースは除外
- 外れ値の検討: 極端な購入金額(標準偏差の3倍超)は検証
- 一貫性チェック: 論理的に矛盾するデータの修正
- 導出変数の作成:
- 顧客ロイヤルティスコア: 購入頻度×客単価×リピート率に基づく指標
- カテゴリ多様性指標: 購入カテゴリの多様さを示す指標
- リマーケティング反応性: 過去のキャンペーンへの反応率
- サンプル構成:
- 性別: 男性45%、女性55%
- 年齢層分布: 20代30%、30代25%、40代20%、その他25%
- 地域分布: 首都圏60%、その他40%
12.3 基本クロス集計
主要な変数間の関係を探索するための基本的なクロス集計を実施します:
- 年齢層×性別×購入カテゴリのクロス集計:
- 表形式の例(一部抜粋): 性別 年齢層 衣料品 家電 食品・飲料 美容・健康 書籍・メディア 合計 男性 20代 25% 35% 15% 10% 15% 100% 男性 30代 20% 40% 20% 5% 15% 100% 女性 20代 40% 15% 20% 20% 5% 100% 女性 30代 35% 20% 25% 15% 5% 100%
- 主な発見:
- 20代女性は衣料品の購入比率が最も高い(40%)
- 30代男性は家電の購入比率が最も高い(40%)
- 書籍・メディアカテゴリは男性の方が購入比率が高い
- 購入頻度×客単価のクロス集計:
- 表形式の例: 購入頻度 低客単価 中客単価 高客単価 合計 低頻度 60% 30% 10% 100% 中頻度 40% 45% 15% 100% 高頻度 30% 45% 25% 100%
- 主な発見:
- 購入頻度が高いほど、高客単価の割合も増加する傾向
- 中頻度・中客単価のセグメントが最も大きい
- 低頻度購入者の60%は低客単価
- 購入時間帯×年齢層のクロス集計:
- カイ二乗検定結果: χ² = 78.5, df = 20, p < 0.001
- 調整済み標準化残差のヒートマップを作成
- 主な発見:
- 20代は夕方と深夜の購入が有意に多い(残差 +3.2, +4.1)
- 50代以上は朝の時間帯の購入が有意に多い(残差 +2.8)
- 30-40代は昼間の購入が比較的多い(残差 +1.9)
12.4 高度な分析
基本クロス集計の結果を踏まえて、より高度な分析を展開します:
- 多重クロス集計による層別分析:
- 「年齢層×購入カテゴリ」の関係を性別で層別
- 「購入時間帯×購入カテゴリ」の関係を年齢層で層別
- シンプソンのパラドックスの検証
- 対応分析による市場ポジショニング:
- 年齢層×購入カテゴリの対応分析マップ作成
- 解釈:
- 第1軸(寄与率58%): 実用性志向 vs. 感性志向
- 第2軸(寄与率29%): 伝統的 vs. 革新的
- クラスターの特定:「20代女性-衣料品-美容健康」、「30-40代男性-家電-書籍」など
- ログリニアモデルによる交互作用分析:
- 「性別×年齢層×購入カテゴリ」の最適モデル選択
- AIC比較による最適モデル: [性別×購入カテゴリ] + [年齢層×購入カテゴリ]
- 結論: 性別と年齢層は購入カテゴリに独立に影響、両者の交互作用効果は小さい
- セグメントプロファイリング:
- 高価値顧客セグメント(高頻度×高客単価)の特徴分析
- 機械学習による顧客セグメント自動分類とクロス集計による検証
12.5 結果の解釈と報告
分析結果に基づく洞察と実践的な推奨事項をまとめます:
- 主要な発見:
- 購入行動における性別・年齢層による明確な嗜好の違い
- 購入頻度と客単価の正の相関関係
- 時間帯による顧客層の変化パターン
- 高価値セグメントの明確なプロファイル特定
- ビジネスインプリケーション:
- ターゲットセグメント別のマーケティング戦略
- 20代女性向け: 衣料品・美容カテゴリの夕方~深夜時間帯プロモーション
- 30-40代男性向け: 家電・デジタル製品の昼間時間帯プロモーション
- クロスセル機会の特定
- 「衣料品」購入者への「美容・健康」商品のレコメンデーション
- 「家電」購入者への「書籍・メディア」カテゴリのクロスセル
- 時間帯別マーケティング最適化
- 時間帯別にウェブサイト表示内容を最適化
- EDM配信時間の顧客セグメント別最適化
- ターゲットセグメント別のマーケティング戦略
- 可視化と共有:
- エグゼクティブサマリーダッシュボードの作成
- インタラクティブなクロス集計表とヒートマップの共有
- 年齢層×性別×カテゴリのモザイクプロットによる視覚的プレゼンテーション
- 追加調査の方向性:
- 特定セグメントへの定性調査によるインサイト深堀り
- 購買行動の時系列変化の分析
- 競合他社顧客との比較分析
この実践演習を通じて、クロス集計分析の全過程(問題設定から解釈・報告まで)を体系的に理解することができます。実際の業務では、分析の目的や利用可能なデータに応じて、このプロセスをカスタマイズしながら適用することが重要です。



