パレート分布とべき分布は、どちらも確率論と統計学において重要な役割を果たす分布ですが、その関係性と違いについて深く理解することは、多くの自然現象や社会経済現象を分析する上で非常に重要です。
1. 基本的な定義と関係性
べき分布(Power-law Distribution)
べき分布は、確率変数Xがある値x以上となる確率P(X ≥ x)が、xのべき乗に反比例する形で表される分布の総称です。
数学的には: P(X ≥ x) ∝ x^(-α)
ここでαは分布の特性を決定する正の定数(べき指数)です。
パレート分布(Pareto Distribution)
パレート分布は、べき分布の特殊なケースであり、イタリアの経済学者ヴィルフレド・パレートにちなんで名付けられました。
数学的には: P(X ≥ x) = (x_m/x)^α(x ≥ x_mの場合)
ここでx_mは最小値パラメータ(スケールパラメータ)で、αは形状パラメータです。
重要な違い:パレート分布はべき分布の一種ですが、すべてのべき分布がパレート分布というわけではありません。パレート分布は特定のパラメータ化と制約(x ≥ x_m)を持つべき分布です。
2. 確率密度関数と累積分布関数

べき分布
確率密度関数(一般形): f(x) ∝ x^(-(α+1))
累積分布関数: F(x) = 1 – C·x^(-α)
パレート分布
確率密度関数: f(x) = (αx_m^α)/(x^(α+1))(x ≥ x_mの場合)
累積分布関数: F(x) = 1 – (x_m/x)^α(x ≥ x_mの場合)
違いの詳細:パレート分布は明確に定義された下限値x_mを持ち、確率密度関数と累積分布関数が厳密に定式化されています。一方、べき分布はより一般的な概念で、特定の形式に限定されない様々な形態を取ることができます。
3. 統計的性質
期待値と分散
べき分布
- 期待値 E[X]:α > 1の場合に有限、そうでなければ発散
- 分散 Var[X]:α > 2の場合に有限、そうでなければ発散
パレート分布
- 期待値 E[X] = (αx_m)/(α-1)(α > 1の場合)
- 分散 Var[X] = (x_m^2·α)/((α-1)^2·(α-2))(α > 2の場合)
重要な観察:どちらの分布も、αの値によっては期待値や分散が存在しない(発散する)場合があります。これは「重い裾」を持つ分布の特徴的な性質です。
モーメント生成関数
パレート分布もべき分布も厳密なモーメント生成関数を持ちません。これは無限の期待値を持つ可能性があるためです。代わりに、特性関数や対数モーメント生成関数が使用されることがあります。
4. 歴史的背景と発見
パレート分布
1896年、イタリアの経済学者ヴィルフレド・パレートが富の分配を研究する過程で発見しました。彼は当初、土地所有の不平等を研究していましたが、この分布が多くの国で富の分配に当てはまることを発見しました。これが有名な「80-20の法則」(パレートの法則)の基礎となりました。
べき分布
べき分布の概念はより広範で、様々な科学者によって異なる文脈で発見されてきました。ジョージ・キングスレー・ジップ(Zipfの法則)、フェリックス・アウエルバッハ(都市規模の法則)など多くの科学者が、異なる現象においてべき分布の存在を確認しています。
歴史的違い:パレート分布は経済学の文脈で特定の現象(富の分配)に関連して発見されましたが、べき分布はより広範な科学的探究を通じて複数の分野で独立に発見されました。
5. 対数スケールでの表現
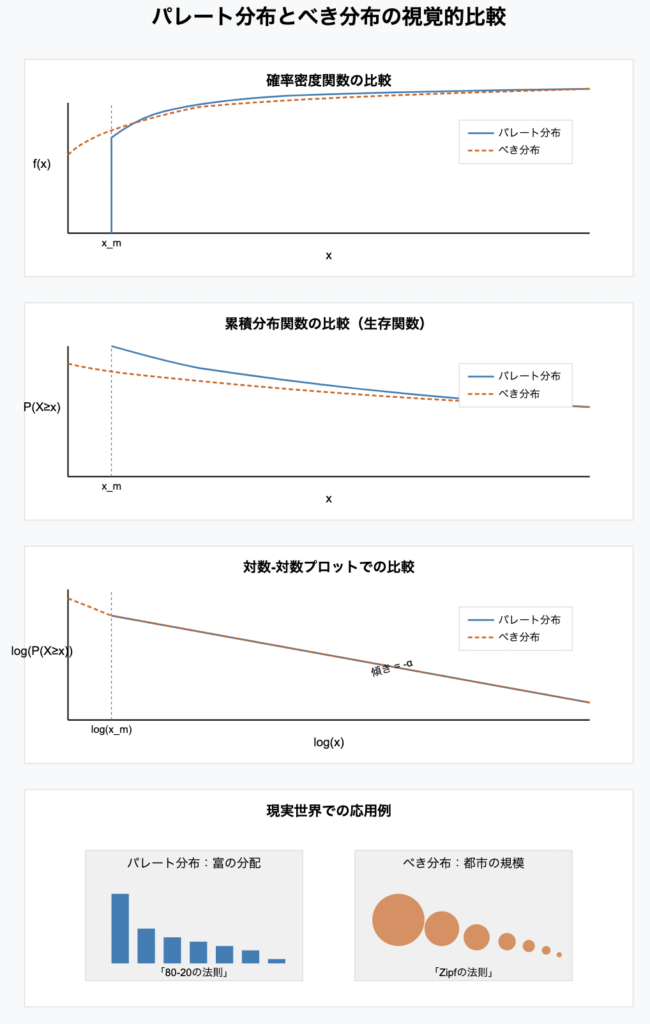
べき分布とパレート分布の特徴的な性質は、対数スケールでの表現で明確になります。
対数-対数プロット
- べき分布:対数-対数プロットでは直線となります。log(P(X ≥ x)) = -α·log(x) + C
- パレート分布:同様に対数-対数プロットでは直線となりますが、x ≥ x_mの範囲に限られます。
視覚的な違い:パレート分布はx_m未満では確率が0となるため、対数-対数プロットではx_mで切断された直線として現れます。一方、一般的なべき分布は異なる範囲で異なるべき指数を持つことができます。
6. 応用分野
パレート分布の応用
- 経済学:富や所得の分配
- ビジネス:売上の80%が20%の顧客からもたらされるという「80-20の法則」
- 保険数理:大きな保険金請求のモデリング
- 品質管理:不良品の発生パターン
べき分布の応用(パレート分布以外)
- 言語学:単語の頻度分布(Zipfの法則)
- 地震学:地震のマグニチュード分布(グーテンベルク-リヒター法則)
- ネットワーク科学:スケールフリーネットワークのノード次数分布
- 都市計画:都市規模の分布
応用の違い:パレート分布は主に経済現象や人間の行動に関連する不平等性に応用される一方、べき分布はより広範な自然現象や複雑系にも適用されます。
7. 数学的な導出と理論的根拠
パレート分布の導出
パレート分布は、最小値x_mを下限とする条件付き確率から導出できます。確率密度関数がべき乗に反比例し、全確率が1になる条件から、規格化定数が決定されます。
べき分布の理論的根拠
べき分布は様々なメカニズムから生じる可能性があります:
- 優先的選択(リッチ・ゲット・リッチャー効果)
- 自己組織化臨界現象
- 乗法的過程と対数正規分布からの漸近的移行
理論的な違い:パレート分布は特定の仮定(最小値の存在と特定のべき乗則)から導かれるのに対し、べき分布はより多様な生成メカニズムを持つことができます。
8. パラメータ推定と統計的検定
パレート分布のパラメータ推定
- 最尤法:α = n/Σlog(x_i/x_m)
- ヒルの推定量:極値理論に基づく推定方法
べき分布の検出と推定
- Clauset-Shalizi-Newmanの方法:最適なx_minとαの推定
- KS検定やAnderson-Darling検定による適合度の評価
推定の違い:パレート分布は明確に定義されたパラメータを持つため、標準的な統計手法で推定可能です。一方、一般的なべき分布では、べき則が始まる閾値の推定や、複数のべきレジームの検出など、より複雑な問題が生じます。
9. 極値理論との関連
パレート分布は極値理論において重要な役割を果たします。特に、一般化パレート分布(GPD)は閾値を超える値のモデリングに使用されます。
一方、一般的なべき分布は極値理論の文脈では直接扱われないことが多いですが、重い裾を持つ分布として関連性があります。
理論的関連性の違い:パレート分布は極値理論の枠組みでより明確に位置づけられています。
10. 他の分布との関係
パレート分布と関連分布
- 対数正規分布:裾の挙動が異なる
- バーの分布:パレート分布の一般化
- F分布:特定のパラメータではパレート分布と関連
べき分布と関連分布
- Zipf分布:離散的なべき分布
- 切断べき分布:上限と下限を持つべき分布
- ツイストべき分布:異なる領域で異なるべき指数を持つ
関連性の違い:パレート分布は特定の確率分布族との明確な関係を持ちますが、べき分布はより広範な分布の性質を表す概念であるため、様々な分布との関係が研究されています。
11. 実世界のデータ分析での留意点
パレート分布の適合
- 最小値パラメータx_mの選択が重要
- αが1に近い場合、期待値の推定が不安定になる可能性
べき分布の適合
- べき則領域の正確な同定が難しい
- データの範囲が限られている場合、対数正規分布などとの区別が困難
実践上の違い:パレート分布は明確なモデルとして適合させやすい一方、一般的なべき分布の検出は複数のモデルとの比較や詳細な統計的検証を必要とすることが多いです。
12. 計算機シミュレーションと乱数生成
パレート分布からの乱数生成
逆変換法を用いて簡単に生成できます: X = x_m / (1-U)^(1/α)(Uは[0,1)の一様乱数)
べき分布からの乱数生成
べき分布の具体的な形式によって手法が異なります。一般的なべき関数の乱数生成は、分布の定義域や正規化定数に依存します。
計算上の違い:パレート分布は標準的な手法で効率的に乱数生成できますが、一般的なべき分布では分布の詳細な特徴に応じた手法が必要です。
13. 理論的な拡張と変種
パレート分布の拡張
- 一般化パレート分布(GPD)
- 両側パレート分布
- Burr分布
べき分布の拡張と変種
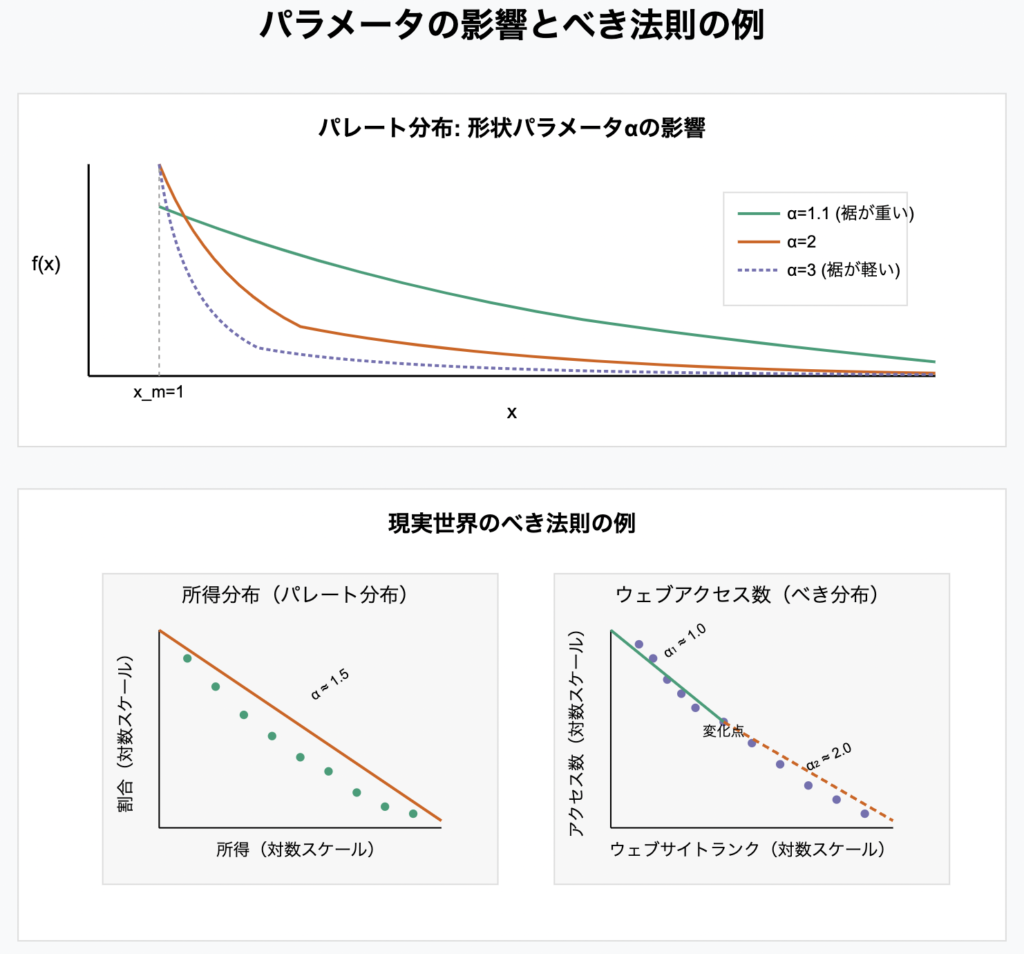
- 折れ曲がりべき分布(特定の値で指数が変化)
- 指数切断べき分布(大きな値で指数関数的に減衰)
- 階層的べき分布
拡張の違い:パレート分布は主に特定のパラメータを追加することで拡張されますが、べき分布の変種はより多様で、異なる現象の複雑な性質を捉えるために開発されています。
結論
パレート分布とべき分布は密接に関連していますが、その違いを理解することは重要です:
- 包含関係:パレート分布はべき分布の特殊なケースです。
- 定式化:パレート分布は明確に定義されたパラメータと数式を持ちますが、べき分布はより一般的な概念です。
- 応用領域:パレート分布は主に経済現象や不平等性に関連しますが、べき分布はより広範な自然・社会現象に現れます。
- 統計的扱い:パレート分布はより標準的な統計手法で扱えますが、一般的なべき分布の識別と推定はより複雑です。
これらの分布の適切な理解と適用は、複雑系、経済学、自然科学などの多くの分野で重要な洞察をもたらします。



