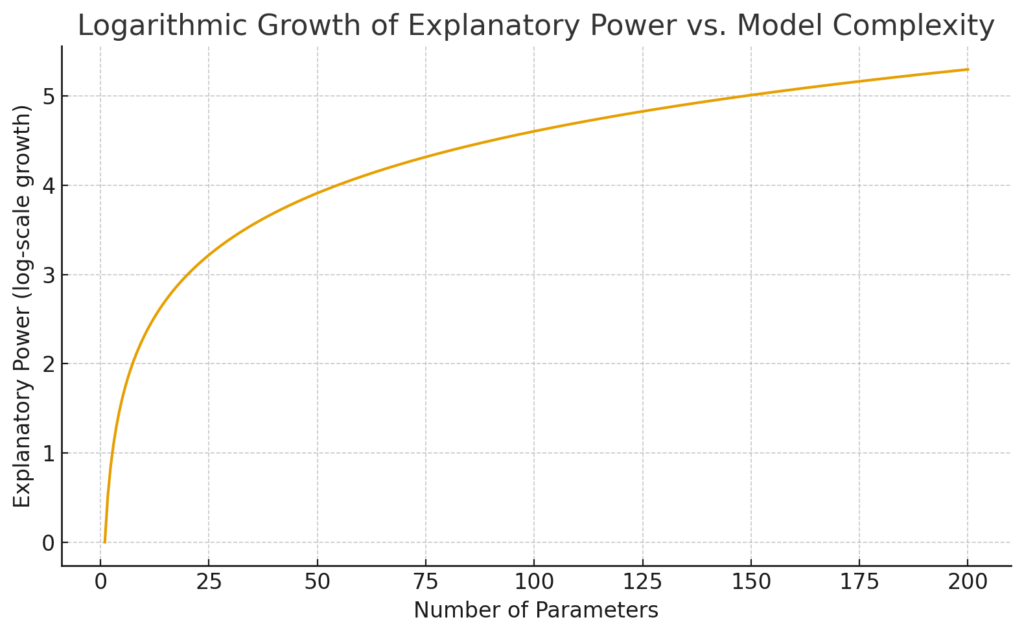
私たちはしばしば、「モデルのパラメータを増やせば説明力がどんどん上がる」と考えがちだ。しかし現実は違う。パラメータ数と説明力の関係をグラフに描けば、真っ直ぐ右肩上がりになるのではなく、対数カーブのようにゆっくりとしか上昇しない。むしろ、最初は急に効くが、やがて伸びは鈍化し、ついには飽和する。
この“対数的な逓減”こそが、オッカムの剃刀が支持される深層的な理由であり、ロバスト性の源泉でもある。
パラメータ追加は「最初の数個」が圧倒的に効く
モデルがまっさらな状態のとき、少数のパラメータが生む説明力は劇的だ。
直線に 1 つの曲率を足せば放物線になり、そこにもう 1 つ自由度を加えれば三次曲線になる。これは世界に立ち現れる構造を一段階ずつ掴むようなもので、少数パラメータは“本質的な形”を拾う力が強い。
だが、10 個、100 個とパラメータが増える頃には状況が変わる。
追加パラメータで得られるのは、もはや新しい構造ではなく“微調整”に過ぎない。
ノイズを吸収したり、局所的な揺らぎをなぞることに使われ、全体的な説明力の伸びは急速に小さくなる。
説明力が対数カーブになる数学的な理由
この「逓減」は単なる感覚ではない。
情報理論・統計学・学習理論のどこから見ても、説明力は対数的にしか増えない。
1. 情報量の観点:追加パラメータの“情報効率”は O(1/k) まで落ちる
データの持つ本質的な情報量には限界がある。
つまり、すでに主要構造を説明してしまえば、残された情報は“細部の雑味”に過ぎない。
そのため、追加されるパラメータが吸収できる情報は、
O(log k) または O(1/k) といった形で急速に低下し、対数的な伸びに変わる。
2. 統計モデル選択:BICは log(n) の壁を示す
ベイズ統計に登場する BIC は、モデルの複雑さに (k/2) log n のペナルティを課す。
裏返せば、データ量 n が一定なら、説明力として有効に使えるパラメータ数は log(n) 程度しかない。
どれだけ複雑なモデルを用意しても、“本当に生きるパラメータ”は対数的に頭打ちだ。
3. 学習理論:汎化誤差は log(仮説集合) で効く
PAC 学習や VC 次元の枠組みでは、汎化誤差の上限がよく
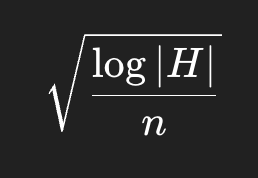
という形で現れる。
仮説集合 |H| はパラメータ数 k に対して指数的に増えるため、
効果としては log |H| ≈ k の“対数的効き方”になる。
増やせば増やすほど当てはまりはよくなるが、汎化性能の改善は急速に細る。
では、対数的にしか伸びないと何が起きるのか?
“説明力の便益”はゆっくりになるのに、“過学習リスク”だけが加速度的に大きくなる。
この非対称性が、オッカムの剃刀の要点だ。
- 複雑にすると得られるもの:微弱な改善(対数的)。
- 複雑にすることで失うもの:ロバスト性の劣化(線形〜指数的)。
つまり、パラメータを増やすほど、
“得るものは小さく、失うものは大きくなる” 構造が必然的に生まれる。
この構造こそが、
単純なモデルの方が“壊れにくい”
=ノイズに対してロバスト
という性質に直結する。
オッカムの剃刀は、哲学ではなく“統計の帰結”である
しばしば、オッカムの剃刀は哲学的スローガンとして扱われる。
しかし本質はむしろ逆だ。
- 情報理論が示す「追加情報の急速な逓減」
- ベイズ統計が見せる「複雑さの対数的限界」
- 学習理論が示す「汎化誤差の log コントロール」
これらが重なることで、
複雑さ → 説明力の伸びが対数カーブで飽和する
という事実が浮き彫りになる。
つまりオッカムの剃刀は、
「単純な説明の方が真に近い確率が高い」
という哲学的主張ではなく、
「複雑さの便益が対数的に弱り、リスクが線形〜指数的に増える」
という数学的帰結なのである。
最後に:なぜ“対数カーブ”がこんなにも強力なのか
対数関数は、初速は鋭いが、後半はほとんど伸びない。
まさにモデル複雑化の宿命そのものだ。
- 最初のパラメータで構造を掴む
- 次の数個で大枠を固める
- それ以降は、ノイズとの綱引きになる
- この極端な非線形構造こそが、
- 「シンプルな方が強い」
- という長年の経験則を、理論的に支えている。



