Toward Relational‑Topological Semantics:
Rethinking Meaning Beyond Cosine Similarity in Large Language Models
Author: Yoshiyuki Hongoh
Abstract
Current large language models (LLMs) encode lexical items as fixed‑dimensional vectors in a high‑dimensional space and approximate semantic relatedness by cosine similarity. While effective for many tasks, this scalar measure collapses richer structures that live between words: context‑dependent, probabilistic networks of relations whose geometry is not Euclidean but topological and categorical. This position paper introduces a two‑level framework for analysing premises—segmentation (definitional partitions) and inclusion (contextual framing)—and argues that meaning emerges from the configuration of relations across these levels, not from isolated token vectors. We outline a research agenda for relational‑topological semantics and sketch how future models might operationalise it.
1 Introduction
Large language models have achieved remarkable fluency by learning distributional representations of words, phrases and sentences. Yet their reliance on cosine similarity limits their capacity to represent (i) the dynamic re‑framing of concepts across contexts and (ii) the probabilistic dispersion of relations between the same pair of words under different premises.
An illustrative case is the statement “AI is an efficiency technology.” In a corporate context, “AI” is framed inside the room (premise) “Productivity”; in a labour‑rights context, the very same “AI” may be reframed within “Surveillance” or “Job Displacement.” A single embedding for AI and efficiency cannot simultaneously accommodate these opposed inclusions without mixing them in opaque ways.
This paper (a) formalises that intuition, (b) summarises limitations of current embedding‑centred semantics, and (c) proposes a relational‑topological research path.
2 Background
2.1 Premise Levels: Segmentation vs Inclusion
We adopt a building metaphor.
- Segmentation (Level 1, “ground floor”): concepts are defined via mutually exclusive partitions (e.g., AI vs non‑AI).
- Inclusion (Level 2, “upper floors”): those segmented rooms are then housed inside broader frames (e.g., Efficiency, Ethics, Surveillance).
Traditional logic expresses premises as membership (A ∈ B) and uses syllogistic composition (if B ⊆ C then A ⊆ C). Our earlier dialogue recast syllogisms as containment arrows in a tower: floors are sets, arrows are premises.
2.2 Embedding Similarity and Its Limits
Cosine similarity presumes static, isotropic distances; it cannot represent that AI may be near efficiency in one discourse but near control in another. Contextualised embeddings (e.g., transformer hidden states) adjust meaning per sentence, yet the comparison metric remains a pointwise dot‑product, not an explicit relation object that can fork across frames.
3 Relational‑Topological Semantics
We propose modelling meaning as morphisms (arrows) between conceptual regions. A word’s “meaning” is the family of arrows it participates in, together with the probability distribution over those arrows across discourse contexts.
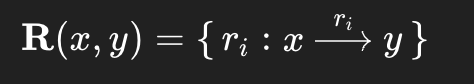
be the set of relational labels (e.g., causes, is‑a, owned‑by, frames, critiques) observed across a corpus, each with empirical weight p_i.
Definition 2 (Topological Frame Space). Let (C, τ) be a topology whose open sets are context‑dependent frames (Efficiency, Surveillance, …). A relational profile is continuous if arrow weights vary smoothly under context shifts inside τ.
Under this view, cosine similarity measures only the zeroth‑order coincidence of profiles, ignoring τ and p_i.
4 Illustrative Example
| Context Frame (open set) | Dominant Arrow | Probability |
|---|---|---|
| Corporate Strategy | AI → boosts → Efficiency | .72 |
| Labour Ethics | AI → threatens → Jobs | .61 |
| State Security | AI → enables → Surveillance | .58 |
The same token pair (AI, Efficiency) has high weight only in the first frame. A relational‑topological model would keep these arrow weights separate and reason with them conditionally; a cosine‑based model blends them.
5 Research Agenda
- Data: Extract multi‑relational triples with contextual labels; build probabilistic arrow sets.
- Representation: Investigate graph neural nets over typed edges; explore category‑theoretic embeddings where arrows are first‑class citizens.
- Learning Objective: Move from maximising token likelihoods to preserving arrow–context distributions.
- Inference: Implement dynamic frame‑shifting: given a question, select or construct the topology slice relevant to that discourse.
- Evaluation: Design tasks that require premise re‑framing (e.g., argument rebuttal, context transfer).
6 Implications
- Explainability: Relations as explicit objects yield traceable reasoning paths (“AI entered Surveillance via arrow enables”).
- Robustness: Keeping alternative frames separate prevents spurious averaging.
- Cognitive Alignment: Mirrors human capacity to reposition concepts by asking “in what sense?”
7 Future Work
- Formalise continuity conditions for frame transitions.
- Explore topos‑inspired logics that integrate segmentation (sub‑object classifiers) and inclusion (geometric morphisms).
- Prototype a frame‑aware language model and benchmark on dynamic‑premise tasks.
8 Conclusion
Meaning lives in the probabilistic, context‑driven relations between concepts, not in isolated vectors. By elevating relational profiles and topological frames to first‑class citizens, we can move beyond cosine similarity toward models that think with premises—models capable of restructuring their own semantic space in response to new questions.
References (selected)
- Gärdenfors, P. Conceptual Spaces (2000).
- Coecke, B., Sadrzadeh, M., & Clark, S. “Categorical Compositional Distributional Semantics.” (2010).
- Tenenbaum, J.B., et al. “How to Grow a Mind: Statistics, Structure, and Abstraction.” Science (2011).
- Hedges, J. “Towards a Category‑Theoretic Foundation for Natural‑Language Semantics.” arXiv (2023).
This draft is intended as a seed document. Sections 4–7 require empirical detail and formal proofs. Feedback and collaboration are welcome.



